Christopher Körber

Agile networks with fast adaptation and reconfiguration capabilities are required for sustainable provisioning of high-quality services with high availability. We propose a new methodical framework for short-time network control based on quantum computing (QC) and integer linear program (ILP) models, which has the potential of realizing a real-time network automation. Finally, we study the approach's feasibility with the state-of-the-art quantum annealer D-Wave Advantage 5.2 in case of an example network and provide scaling estimations for larger networks. We embed network problems in quadratic unconstrained binary optimization (QUBO) form for networks of up to 6 nodes. We further find annealing parameters that obtain feasible solutions that are close to a reference solution obtained by classical ILP-solver. We estimate, that a real-sized network with 12 to 16 nodes require a quantum annealing (QA) hardware with at least 50000 qubits or more.

Lattice QCD calculations of two-nucleon interactions have been underway for about a decade, but still haven't reached the pion mass regime necessary for matching onto effective field theories and extrapolating to the physical point. Furthermore, results from different methods, including the use of the Luscher formalism with different types of operators, as well as the HALQCD potential method, do not agree even qualitatively at very heavy pion mass. We investigate the role that different operators employed in the literature may play on the extraction of spectra for use within the Luscher method. We first explore expectations from Effective Field Theory solved within a finite volume, for which the exact spectrum may be computed given different physical scenarios. We then present preliminary lattice QCD results for two-nucleon spectra calculated using different operators on a common lattice ensemble.

The Deep Underground Neutrino Experiment (DUNE) is an upcoming neutrino oscillation experiment that is poised to answer key questions about the nature of neutrinos. Lattice QCD has the ability to make significant impact upon DUNE, beginning with computations of nucleon-neutrino interactions with weak currents. Nucleon amplitudes involving the axial form factor are part of the primary signal measurement process for DUNE, and precise calculations from LQCD can significantly reduce the uncertainty for inputs into Monte Carlo generators. Recent calculations of the nucleon axial charge have demonstrated that sub-percent precision is possible on this vital quantity. In these proceedings, we discuss preliminary results for the CalLat collaboration's calculation of the axial form factor of the nucleon. These computations are performed with Möbius domain wall valence quarks on HISQ sea quark ensembles generated by the MILC and CalLat collaborations. The results use a variety of ensembles including several at physical pion mass.

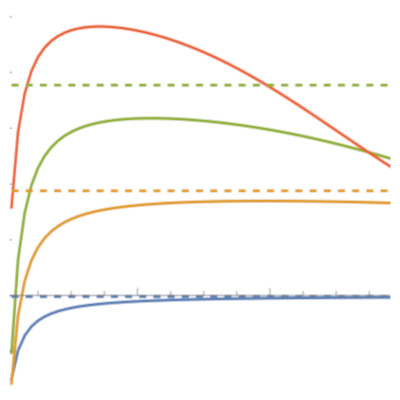
Excited state contamination remains one of the most challenging sources of systematic uncertainty to control in lattice QCD calculations of nucleon matrix elements and form factors. Most lattice QCD collaborations advocate for the use of high-statistics calculations at large time separations ($t_{\mathrm{sep}} \geq 1$ fm) to combat the signal-to-noise degradation. In this work we demonstrate that, for the nucleon axial charge, $g_A$, the alternative strategy of utilizing a large number of relatively low-statistics calculations at short to medium time separations ($0.2\leq t_{\mathrm{sep}} \leq1$ fm), combined with a multi-state analysis, provides a more robust and economical method of quantifying and controlling the excited state systematic uncertainty, including correlated late-time fluctuations that may bias the ground state. We show that two classes of excited states largely cancel in the ratio of the three-point to two-point functions, leaving the third class, the transition matrix elements, as the dominant source of contamination. On an $m_\pi \approx 310$ MeV ensemble, we observe the expected exponential suppression of excited state contamination in the Feynman-Hellmann correlation function relative to the standard three-point function; the excited states of the regular three-point function reduce to the 1% level for $t_{\mathrm{sep}} >2$ fm while, for the Feynman-Hellmann correlation function, they are suppressed to 1% at $t_{\mathrm{sep}} \approx 1$ fm. Independent analyses of the three-point and Feynman-Hellmann correlators yield consistent results for the ground state. However, a combined analysis allows for a more detailed and robust understanding of the excited state contamination, improving the demonstration that the ground state parameters are stable against variations in the excited state model, the number of excited states, and the truncation of early-time or late-time numerical data.

We report on a subpercent scale determination using the omega baryon mass and gradient-flow methods. The calculations are performed on 22 ensembles of Nf=2+1+1 highly improved, rooted staggered sea-quark configurations generated by the MILC and CalLat Collaborations. The valence quark action used is Möbius domain wall fermions solved on these configurations after a gradient-flow smearing is applied with a flowtime of tgf=1 in lattice units. The ensembles span four lattice spacings in the range 0.06≲a≲0.15  fm, six pion masses in the range 130≲mπ≲400  MeV and multiple lattice volumes. On each ensemble, the gradient-flow scales t0/a2 and w0/a and the omega baryon mass amΩ are computed. The dimensionless product of these quantities is then extrapolated to the continuum and infinite volume limits and interpolated to the physical light, strange and charm quark mass point in the isospin limit, resulting in the determination of t0=0.1422(14)  fm and w0=0.1709(11)  fm with all sources of statistical and systematic uncertainty accounted for. The dominant uncertainty in both results is the stochastic uncertainty, though for t0 there are comparable continuum extrapolation uncertainties. For w0, there is a clear path for a few-per-mille uncertainty just through improved stochastic precision, as recently obtained by the Budapest-Marseille-Wuppertal Collaboration.

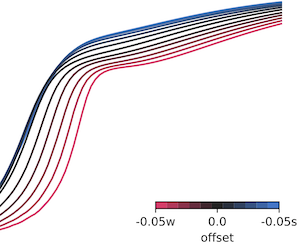
While quantum computing proposes promising solutions to computational problems not accessible with classical approaches, due to current hardware constraints, most quantum algorithms are not yet capable of computing systems of practical relevance, and classical counterparts outperform them. To practically benefit from quantum architecture, one has to identify problems and algorithms with favorable scaling and improve on corresponding limitations depending on available hardware. For this reason, we developed an algorithm that solves integer linear programming problems, a classically NP-hard problem, on a quantum annealer, and investigated problem and hardware-specific limitations. This work presents the formalism of how to map ILP problems to the annealing architectures, how to systematically improve computations utilizing optimized anneal schedules, and models the anneal process through a simulation. It illustrates the effects of decoherence and many body localization for the minimum dominating set problem, and compares annealing results against numerical simulations of the quantum architecture. We find that the algorithm outperforms random guessing but is limited to small problems and that annealing schedules can be adjusted to reduce the effects of decoherence. Simulations qualitatively reproduce algorithmic improvements of the modified annealing schedule, suggesting the improvements have origins from quantum effects.

We report on the first application of the stochastic Laplacian Heaviside method for computing multi-particle interactions with lattice QCD to the two-nucleon system. Like the Laplacian Heaviside method, this method allows for the construction of interpolating operators which can be used to construct a positive definite set of two-nucleon correlation functions, unlike nearly all other applications of lattice QCD to two nucleons in the literature. It also allows for a variational analysis in which optimal linear combinations of the interpolating operators are formed that couple predominantly to the eigenstates of the system. Utilizing such methods has become of paramount importance in order to help resolve the discrepancy in the literature on whether two nucleons in either isospin channel form a bound state at pion masses heavier than physical, with the discrepancy persisting even in the $SU(3)$-flavor symmetric point with all quark masses near the physical strange quark mass. This is the first in a series of papers aimed at resolving this discrepancy. In the present work, we employ the stochastic Laplacian Heaviside method without a hexaquark operator in the basis at a lattice spacing of $a\sim0.086$~fm, lattice volume of $L=48 a \simeq 4.1$~fm and pion mass $m_\pi \simeq 714$~MeV. With this setup, the observed spectrum of two-nucleon energy levels strongly disfavors the presence of a bound state in either the deuteron or dineutron channel.

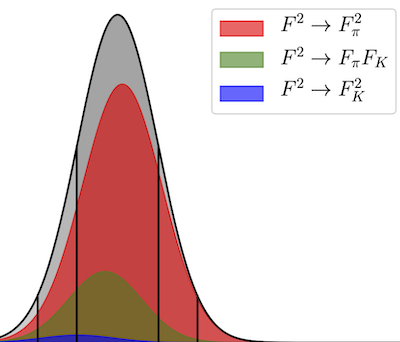
We report the results of a lattice QCD calculation of $F_K/F_\pi$ using Möbius Domain-Wall fermions computed on gradient-flowed $N_f=2+1+1$ HISQ ensembles. The calculation is performed with five values of the pion mass ranging from $130 \lesssim m_\pi \lesssim 400$~MeV, four lattice spacings of $a\sim 0.15, 0.12, 0.09$ and $0.06$~fm and multiple values of the lattice volume. The interpolation/extrapolation to the physical pion and kaon mass point, the continuum, and infinite volume limits are performed with a variety of different extrapolation functions utilizing both the relevant mixed-action effective field theory expressions as well as discretization-enhanced continuum chiral perturbation theory formulas. We find that the $a\sim0.06$~fm ensemble is helpful, but not necessary to achieve a sub-percent determination of $F_K/F_\pi$. We also include an estimate of the strong isospin breaking corrections and arrive at a final result of $F_{\hat{K}^+}/F_{\hat{\pi}^+} = 1.1942(45)$ with all sources of statistical and systematic uncertainty included. This is consistent with the FLAG average value, providing an important benchmark for our lattice action. Combining our result with experimental measurements of the pion and kaon leptonic decays leads to a determination of $|V_{us}|/|V_{ud}| = 0.2311(10)$.

EspressoDB is a programmatic object-relational mapping (ORM) data management framework implemented in Python and based on the Django web framework. EspressoDB was developed to streamline data management, centralize and promote data integrity, while providing domain flexibility and ease of use. It is designed to directly integrate in utilized software to allow dynamical access to vast amount of relational data at runtime. Compared to existing ORM frameworks like SQLAlchemy or Django itself, EspressoDB lowers the barrier of access by simplifying the project setup and provides further features to satisfy uniqueness and consistency over multiple data dependencies. In contrast to software like DVC, VisTrails, or Taverna, which describe the workflow of computations, EspressoDB rather interacts with data itself and thus can be used in a complementary spirit.

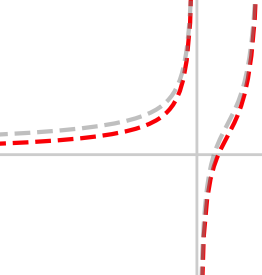
Contact interactions can be used to describe a system of particles at unitarity, contribute to the leading part of nuclear interactions and are numerically non-trivial because they require a proper regularization and renormalization scheme. We explain how to tune the coefficient of a contact interaction between non-relativistic particles on a discretized space in 1, 2, and 3 spatial dimensions such that we can remove all discretization artifacts. By taking advantage of a latticized Lüscher zeta function, we can achieve a momentum-independent scattering amplitude at any finite lattice spacing.

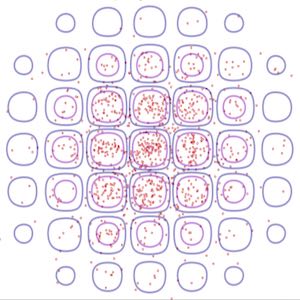
The Hubbard model arises naturally when electron-electron interactions are added to the tight-binding descriptions of many condensed matter systems. For instance, the two-dimensional Hubbard model on the honeycomb lattice is central to the ab initio description of the electronic structure of carbon nanomaterials, such as graphene. Such low-dimensional Hubbard models are advantageously studied with Markov chain Monte Carlo methods, such as Hybrid Monte Carlo (HMC). HMC is the standard algorithm of the lattice gauge theory community, as it is well suited to theories of dynamical fermions. As HMC performs continuous, global updates of the lattice degrees of freedom, it provides superior scaling with system size relative to local updating methods. A potential drawback of HMC is its susceptibility to ergodicity problems due to so-called exceptional configurations, for which the fermion operator cannot be inverted. Recently, ergodicity problems were found in some formulations of HMC simulations of the Hubbard model. Here, we address this issue directly and clarify under what conditions ergodicity is maintained or violated in HMC simulations of the Hubbard model. We study different lattice formulations of the fermion operator and provide explicit, representative calculations for small systems, often comparing to exact results. We show that a fermion operator can be found which is both computationally convenient and free of ergodicity problems.

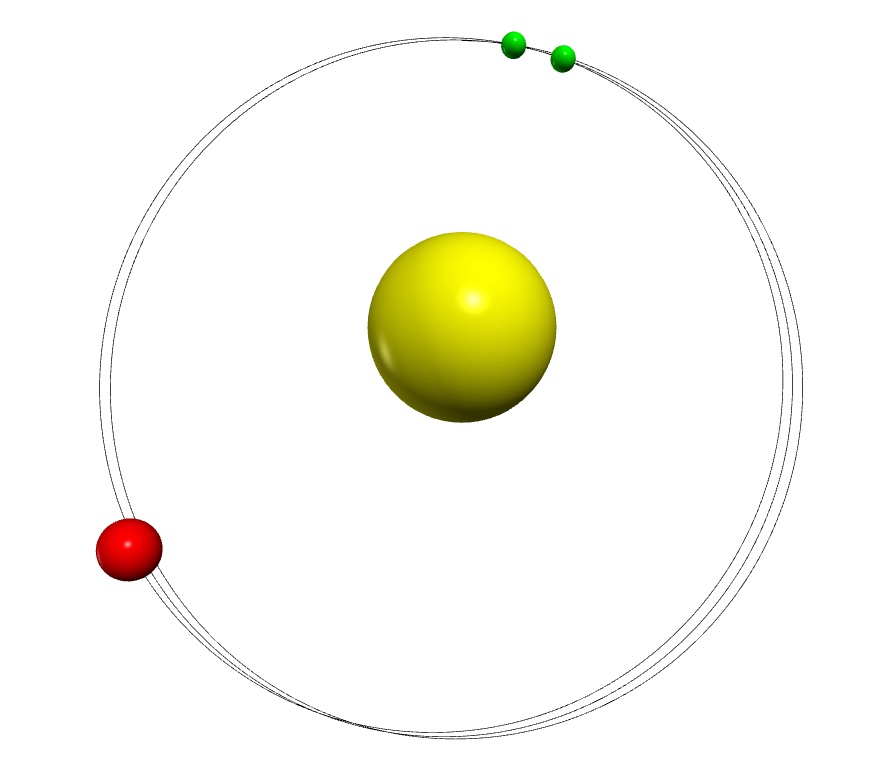
In our previous publication "A primer to numerical simulations: The perihelion motion of Mercury", we describe a scenario on how to teach numerical simulations to high school students. In this online article, we describe our motivation and the experiences we have made during the two summer schools where we have presented this course.

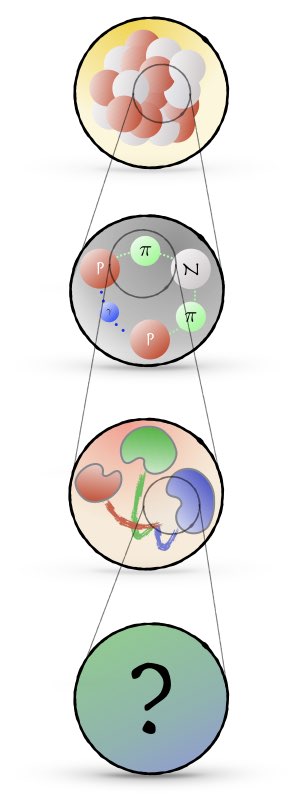
Fundamental symmetries (and their violations) play a significant role in active experimental searches of Beyond the Standard Model (BSM) signatures. An example of such phenomena is the neutron Electric Dipole Moment (EDM), a measurement of which would be evidence for Charge-Parity (CP) violation not attributable to the basic description of the Standard Model (SM). Another example is the strange scalar quark content of the nucleon and its coupling to Weakly Interacting Massive Particles (WIMPs), which is a candidate model for Dark Matter (DM). The theoretical understanding of such processes is fraught with uncertainties and uncontrolled approximations. On the other hand, methods within nuclear physics, such as Lattice Quantum Chromodynamics (LQCD) and Effective Field Theories (EFT), are emerging as powerful tools for calculating non-perturbatively various types of nuclear and hadronic observables. This research effort will use such tools to investigate phenomena related to BSM physics induced within light nuclear systems. As opposed to LQCD which deal with quarks and gluons, in Nuclear Lattice Effective Field Theory (NLEFT) individual nucleons—protons and neutrons—form the degrees of freedom. From the symmetries of Quantum Chromodynamics (QCD), one can derive the most general interaction-structures allowed on the level of these individual nucleons. In general, this includes an infinite number of possible interactions. Utilizing the framework of EFTs, more specifically for this work Chiral Perturbation Theory (χPT), one can systematically expand the nuclear behavior in a finite set of relevant nuclear interactions with a quantifiable accuracy. Fundamental parameters of this theory are related to experiments or LQCD computations. Using this set of effective nuclear interaction-structures, one can describe many-nucleon systems by simulating the quantum behavior of each involved individual nucleon. The 'ab initio' method NLEFT introduces a spatial lattice which is finite in its volume (FV) and allows to exploit powerful numerical tools in the form of statistical Hybrid Monte Carlo (HMC) algorithms. The uncertainty of all three approximations—the statistical sampling, the finite volume and the discretization of space—can be analytically understood and used to make a realistic and accurate estimation of associated uncertainty. In the first part of the thesis, χPT is used to derive nuclear interactions with a possible BSM candidate up to Next-to-Leading Order (NLO) in the specific case of scalar interactions between DM and quarks or gluons. Following this analysis, Nuclear Matrix- Elements (NMEs) are presented for light nuclei (2H, 3He and 3H), including a complete uncertainty estimation. These results will eventually serve as the benchmark for the many-body computations. In the second part of this thesis, the framework of NLEFT is briefly presented. It is shown how one can increase the accuracy of NLEFT by incorporating few-body forces in a non-perturbative manner. Finite-Volume (FV) and discretization effects are investigated and estimated for BSM NME on the lattice. Furthermore, it is displayed how different boundary conditions can be used to decrease the size of FV effects and extend the scope of available lattice momenta to the range of physical interest.

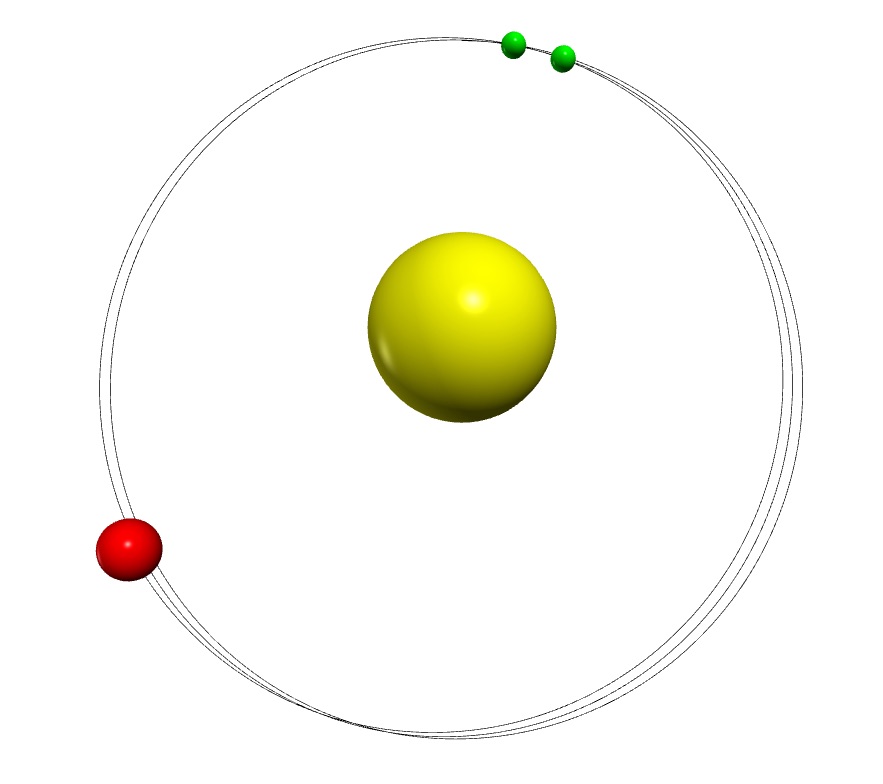
Numerical simulations are playing an increasingly important role in modern science. In this work it is suggested to use a numerical study of the famous perihelion motion of the planet Mercury (one of the prime observables supporting Einsteins General Relativity) as a test case to teach numerical simulations to high school students. The paper includes details about the development of the code as well as a discussion of the visualization of the results. In addition a method is discussed that allows one to estimate the size of the effect as well as the uncertainty of the approach a priori. At the same time this enables the students to double check the results found numerically. The course is structured into a basic block and two further refinements which aim at more advanced students.

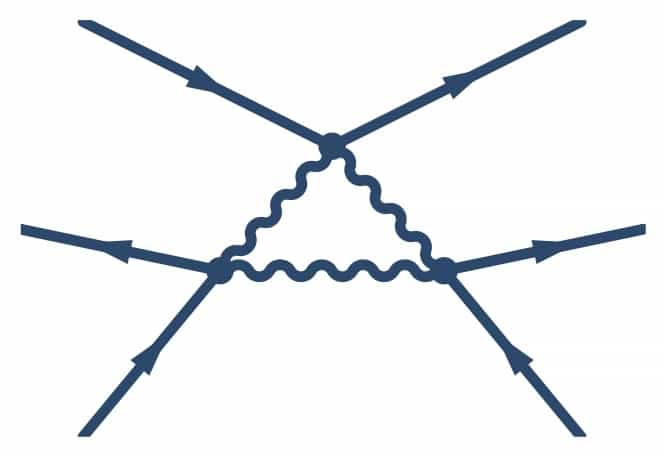
We present a general auxiliary field transformation which generates effective interactions containing all possible N-body contact terms. The strength of the induced terms can analytically be described in terms of general coefficients associated with the transformation and thus are controllable. This transformation provides a novel way for sampling 3- and 4-body (and higher) contact interactions non-perturbatively in lattice quantum monte-carlo simulations. We show that our method reproduces the exact solution for a two-site quantum mechanical problem.

We show how lattice Quantum Monte Carlo simulations can be used to calculate electronic properties of carbon nanotubes in the presence of strong electron-electron correlations. We employ the path integral formalism and use methods developed within the lattice QCD community for our numerical work and compare our results to empirical data of the Anti-Ferromagnetic Mott Insulating gap in large diameter tubes.

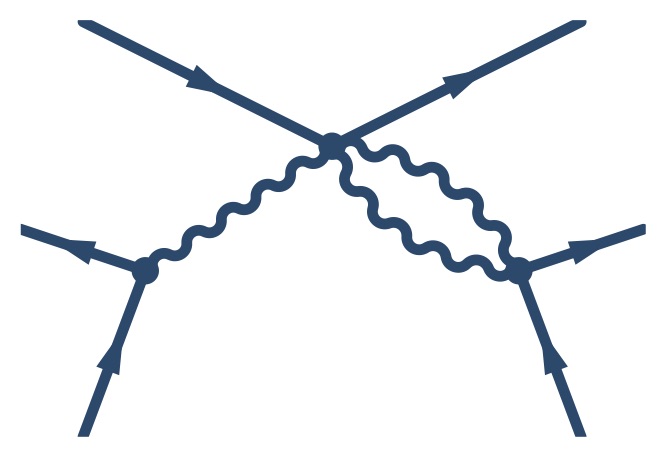
Through the development of many-body methodology and algorithms, it has become possible to describe quantum systems composed of a large number of particles with great accuracy. Essential to all these methods is the application of auxiliary fields via the Hubbard-Stratonovich transformation. This transformation effectively reduces two-body interactions to interactions of one particle with the auxiliary field, thereby improving the computational scaling of the respective algorithms. The relevance of collective phenomena and interactions grows with the number of particles. For many theories, e.g. Chiral Perturbation Theory, the inclusion of three-body forces has become essential in order to further increase the accuracy on the many-body level. In this proceeding, the analytical framework for establishing a Hubbard-Stratonovich-like transformation, which allows for the systematic and controlled inclusion of contact three- and more-body interactions, is presented.

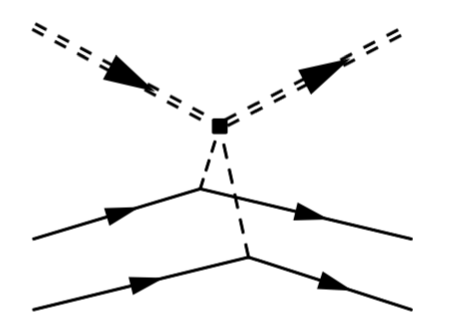
We study the scattering of Dark Matter particles off various light nuclei within the framework of chiral effective field theory. We focus on scalar interactions and include one- and two-nucleon scattering processes whose form and strength are dictated by chiral symmetry. The nuclear wave functions are calculated from chiral effective field theory interactions as well and we investigate the convergence pattern of the chiral expansion in the nuclear potential and the Dark Matter-nucleus currents. This allows us to provide a systematic un- certainty estimate of our calculations. We provide results for $^2$H, $^3$H, and $^3$He nuclei which are theoretically interesting and the latter is a potential target for experiments. We show that two-nucleon currents can be systematically included but are generally smaller than predicted by power counting and suffer from significant theoretical uncertainties even in light nuclei. We demonstrate that accurate high-order wave functions are necessary in order to incorporate two-nucleon currents. We discuss scenarios in which one-nucleon contributions are suppressed such that higher-order currents become dominant.

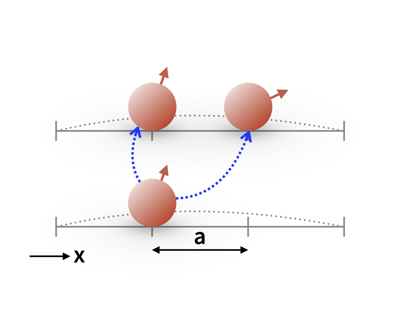
We describe and implement twisted boundary conditions for the deuteron and triton systems within finite volumes using the nuclear lattice EFT formalism. We investigate the finite-volume dependence of these systems with different twist angles. We demonstrate how various finite-volume information can be used to improve calculations of binding energies in such a framework. Our results suggest that with the appropriate twisting of boundaries, infinite-volume binding energies can be reliably extracted from calculations using modest volume sizes with cubic length $L \approx 8–14$ fm. Of particular importance is our derivation and numerical verification of three-body analogs of “i-periodic” twist angles that eliminate the leading-order finite-volume effects to the three-body binding energy.

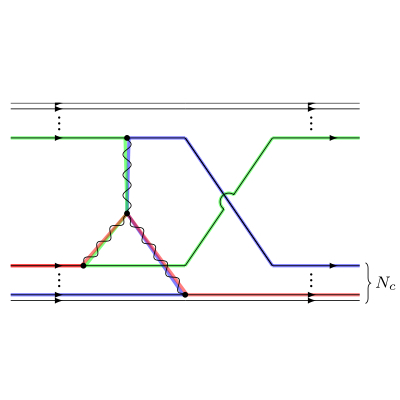
The work tests the consistency of nucleon-nucleon forces derived by two different approximation schemes of Quantum Chromodynamics (QCD)—the chiral perturbation theory ($\chi$PT) and large-Nc QCD. The approximation schemes and the derivation of the potential are demonstrated in this work. The consistency of the chiral potential, derived using the method of unitary transformation, is verified for chiral orders $Q^\nu$ for $\nu = 0,2,4$. Used methods, as well as possible extensions for higher orders, are presented.